7.4 Interval Estimation
Sometimes it is required to find not only a numerical estimation of the parameter of a population, but also to evaluate its accuracy and reliability. It is especially important for a sample with small volume. Generalization of a point estimation of the statistical parameter is an interval estimation - the numerical interval containing the estimated parameter with defined probability.
In definiting
general characteristics of sampled data some error arises. In this case, it is
better to define an interval with the centre equal to the point estimator.
Inside such an interval with given probability there is a true required value of
the estimated parameter of the general population. Such an interval is called
confidence. The confidence interval is a numerical interval which, with the
given probability
![]() ,
include the estimated parameter of a population. Such probability is known as
the confidential probability. The confidential probability
,
include the estimated parameter of a population. Such probability is known as
the confidential probability. The confidential probability
![]() is
a probability which is sufficient for the inference about reliability of the
parameters obtained on the sample. Probability to make an error is called a
significance level:
is
a probability which is sufficient for the inference about reliability of the
parameters obtained on the sample. Probability to make an error is called a
significance level:
![]() (7.19)
(7.19)
For point
(sample) estimation –![]() of a
population’s parameter –
of a
population’s parameter –
![]() with
accuracy (the limiting error) –
with
accuracy (the limiting error) –
![]() , and a
confidential probability –
, and a
confidential probability –
![]() , the
confidence interval –
, the
confidence interval –
![]() is
determined by equality:
is
determined by equality:
![]() (7.20)
(7.20)
The limiting
error (![]() ) and
the mean error (
) and
the mean error (![]() )
have an interrelation:
)
have an interrelation:
![]() (7.21)
(7.21)
where: t – a confidence coefficient.
The limiting error for a small sample is calculated as follows:
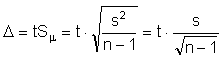 (7.22)
(7.22)
The limiting error also depends on a probability (р) which guarantees such error. On the basis of theorems of Chebyshev and Lyapunov we have the interrelation of a confidence coefficient (t) with a probability (р):
|
Confidence coefficient t |
Probability р |
|
1.0 |
0.683 |
|
1.5 |
0.866 |
|
2.0 |
0.954 |
|
2.5 |
0.987 |
|
3.0 |
0.997 |
If we have a
probability р=0.997, a confidence coefficient t will equal 3, and for an average
we will have an interval:
![]() or
or
![]() .
This is the so-called rule of three
sigma.
In 997 events out of 1000 we can assert that the population mean will not fall
outside the limit of sample mean ± triple mean error of sample.
.
This is the so-called rule of three
sigma.
In 997 events out of 1000 we can assert that the population mean will not fall
outside the limit of sample mean ± triple mean error of sample.
Confidence
coefficient t (or trust’s coefficient) has connection with confidential
probability. This coefficient is defined by the Laplace integral with the
confidential probability
![]() :
:
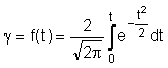 (7.23)
(7.23)
The confidential probability
γ
enables us to form a
confidential bounds (![]() ) of a
random fluctuation of the studied parameter (Q)
for the given sample.
) of a
random fluctuation of the studied parameter (Q)
for the given sample.
Confidential
probability has the following values and significance level (α = 1 –![]() )
corresponding to them:
)
corresponding to them:
|
Confidential probability |
Significance level, α |
|
0,90 |
0,10 or 10 % |
|
0,95 |
0,05 or 5 % |
|
0,99 |
0,01 or 1 % |
The 5% significance level means that in 5 events out of 100 there is a possibility to do an error in calculation of a parameter of a population on sampled data. In other words, in 95 events out of 100, parameters of a population calculated on the sample will lie within the limits of a confidence interval.
For example,
at a shearing of 100 sheep from 1000 heads, the sample mean is 4.5 kg, the
sample standard deviation is 1.3 kg. Find out a limiting error of sample with
probability 0.954 and possible limits of mean shearing from one sheep in
population:
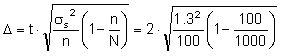 =0.25,
=0.25,
![]() ,
,
![]() ,
,
![]() .
.
The population mean (at shearing of 1000 sheep) can’t be less than 4.25 kg and can’t be more than 4.75 kg with a probability 95.4%.
Let's consider
an example of an estimation of arithmetic mean on a small sample. From a herd of
sheep are selected 17 sheep which were weighed (sample size is n=17). Sample
mean weight is
![]() =60 kg,
and
=60 kg,
and ![]() . Let's calculate a probability of what the population mean is
in interval
. Let's calculate a probability of what the population mean is
in interval ![]() , if a significance level a=
5%. Using the parity:
, if a significance level a=
5%. Using the parity:
![]() (7.24)
(7.24)
and denoting a limiting error as ∆, we find confidential borders of an interval:
![]() .
.
The number of degrees of freedom equals 16. The trust’s coefficient t = 2.12. Therefore:
![]()
Confidential interval is (60-4.7; 60+4.7). With probability 0.95 it is possible to confirm that population mean weight of sheep is in an interval (55.3; 64.7).
Using the formula of limiting error it is possible to define the minimum volume (size) of a sample for which the estimation with needed properties is provided:
–
for selection
with replacement:
![]() (7.25)
(7.25)
–
for selection
without replacement:
![]() (7.26)
(7.26)
Let's consider
characteristics of two independent samples. There are: volume (size) of two
samples - n1, n2, arithmetic mean of two samples -
![]() ,
,
![]() , and
sample variance -
, and
sample variance -
![]() ,
,
![]() .
Summation/subtraction of these samples has equality:
.
Summation/subtraction of these samples has equality:
![]() (7.27)
(7.27)
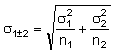 (7.28)
(7.28)