Zadania do samodzielnego rozwiązania
2.1.
Prawdopodobieństwo tego, że statystyczny student nie jest przygotowany do ćwiczeń wynosi p = 1/3. Prowadzący zajęcia wybiera losowo cztery osoby. Niech wartościami zmiennej losowej X będzie liczba osób nie przygotowanych do ćwiczeń spośród wybranych. Podać rozkład tej zmiennej losowej, jej parametry i funkcję dystrybuanty. Obliczyć P(1 < X < 3).Odp. p = 56/81.
2.2.
Zmienna losowa X ma rozkład Poissona z parametrem l=2. Obliczyć i odczytać w tablicach:a) P(X < 2)
b) P(X > 3)
c) P(2 < X < 4)
Odp. a) 0,406; b) 0,323; c) 0,271.
2.3.
Wadliwość produkcji pewnego zakładu wynosi 0,1%. Pobieramy losowo 100 sztuk towaru. Obliczyć prawdopodobieństwo, że wśród nich są co najwyżej dwie sztuki wadliwe.Odp. p = 0,999.
2.4.
Zmienna losowa X ma rozkład dwumianowy przy p = 1/3 i n = 5. Podać tabelę f.r.p., funkcję dystrybuanty oraz obliczyć podstawowe parametry.Odp. E(X) = 5/3; D2(X) = 10/9.
2.5.
Na tarczę, podzieloną na 37 jednakowych pól ponumerowanych numerami: 0, 1, 2, ...,36, rzucamy kulę. Znaleźć f.r.p. i dystrybuantę zmiennej losowej X określonej następująco:X = -
2, jeśli kula padnie na pole o numerze parzystym,X = 0, jeśli kula padnie na pole o numerze nieparzystym,
X = 36, jeśli kula padnie na pole o numerze 0.
2.6.
Obliczyć prawdopodobieństwo, że w pięciu doświadczeniach opisanych w zadaniu 6 co najmniej raz zmienna losowa X przyjmie wartość 36.Odp. p = 0,13.
2.7.
Funkcja gęstości prawdopodobieństwa zmiennej X określona jest wzorem: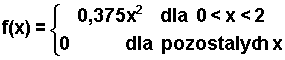
Obliczy
ć wartość średnią i odchylenie standardowe.Odp. E(X) = 1,5; D2(X) = 3/20.
2.8.
Metro na pewnej trasie kursuje ściśle co 5 minut. Jakie jest prawdopodobieństwo, że pasażer przybywający na peron będzie czekał na najbliższy pociąg:a) mniej niż 3 minuty, b)
ponad 4 minuty.Odp. a) 0,6; b) 0,2.
2.9.
Zmienna losowa X ~ N(25; 4). Wyznaczyć prawdopodobieństwo, że zmienna X przyjmie wartość z przedziału <22; 27>.Odp. p = 0,465.
2.10.
Zmienna losowa X ma rozkład N(16;2). Obliczyć prawdopodobieństwa:a) P(
| X - 16 | < 2),b) P(
| X - 16 | < 4),c) P(
| X - 16 | < 6).Jakie wnioski płyną z porównań tych prawdopodobieństw?
Odp. a) 0,683; b) 0,954; c) 0,997.
2.11.
Staż pracy osób na kierowniczych stanowiskach opisuje f.g.p.: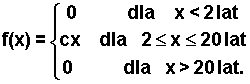
Wyznaczyć stałą c i narysować f.g.p.
Odp. c = 1/198.
2.12.
W pewnym okręgu zaobserwowano w ciągu 25 lat średnio 3 wykolejenia pociągów rocznie. Obliczyć prawdopodobieństwo, że:a) liczba wypadków nie przekroczy dwóch w ciągu roku,
b) w ciągu roku wydarzy się dokładnie 5 wy
padków.Odp. a) 0,423; b) 0,101.
2.13.
Aby wynieść statek kosmiczny na orbitę, system napędowy musi pracować cały czas bez awarii. Prawdopodobieństwo pracy bez awarii jednego z urządzeń tego systemu wynosi 85%. Na pokładzie zainstalowane są 4 takie urządzenia, które pracują niezależnie. Jakie jest prawdopodobieństwo, że system napędowy ulegnie awarii w czasie lotu?Odp. 0,00051.
2.14.
Pewien niewielki zakład transportowy jest w stanie wynająć każdego dnia 2 samochody. Dzienna liczba zgłoszeń klientów chcących nająć samochód jest zmienną losową o rozkładzie Poissona z parametrem l = 1,6.a) Jakie jest prawdopodobieństwo, że nikt nie zgłosi się po samochód?
b) Jaką część stanowią dni, kiedy popyt przekracza możliwości firmy?
c) Jaka jest oczekiwana dzienna lic
zba zgłoszeń klientów?Odp. a) 0,202; b) 0,217 = 21,7%; c) 1,6.
2.15.
Ustalono, że średni roczny błąd prognozy dochodów pewnej firmy ma rozkład normalny ze średnią 31,3% i odchyleniem standardowym 10%. W firmie wykonano roczną prognozę dochodów. Obliczyć prawdopodobieństwo, że błąd prognozy:a) będzie większy od 20% ale nie przekroczy 25%,
b) będzie większy niż 50%.
Odp. a) 0,133; b) 0,029.