![]()
(2.2.2)
ZMIENNA LOSOWA JEDNOWYMIAROWA
I JEJ ROZKŁAD
2.1 Pojęcie zmiennej losowej
Zmienną losową nazywamy funkcję przyporządkowującą każdemu zdarzeniu elementarnemu wartość liczbową. Zmienne losowe oznaczać będziemy X, Y, ..., a wartości (tzw. realizacje) tych
zmiennych: x, y, ... , X: W ® R, lub inaczej: X (vi) = xi, gdzie i = 1, 2, ... W praktyce staramy się, aby to przyporządkowanie było naturalne.Przykład 2.1Przykład 2.2Przykład 2.3Uwaga:Zamiast mówić o prawdopodobieństwie jakiegoś zdarzenia, jako wyniku realizacji doświadczenia, możemy mówić o prawdopodobieństwie tego, że zmienna losowa przyjmuje tę czy inną wartość.
Przykład 2.4W praktyce rozróżniamy dwa typy zmiennej losowej: zmienna losowa skokowa i zmienna losowa ciągła.Zmienna losowa skokowa
to taka zmienna, która przyjmuje tylko niektóre wartości (skończoną lub nieskończoną, ale przeliczalną liczbę wartości). Taką zmienną jest np. liczba osób w grupie studenckiej, liczba przedmiotów wyprodukowanych na danym stanowisku pracy w ciągu jednej zmiany, liczba wadliwych drukarek z przykładu 2.3.Zmienna losowa ciągła
to taka zmienna, która przyjmuje wszystkie wartości z pewnego przedziału liczbowego. Zmienną losową ciągłą jest np.: wzrost, waga, wiek poszczególnych osób, ilość energii elektrycznej zużywanej dziennie przez określony zakład pracy, dochód gospodarstwa rolniczego.2.2 Dystrybuanta zmiennej losowej
Niech x oznacza liczbę rzeczywistą, zaś X zmienną losową. Dla każdego x można obliczyć prawdopodobieństwo tego, że zmienna X przyjmie wartość mniejszą lub równą x:
P(X <= x)
Dystrybuantą zmiennej losowej X nazywamy funkcję F określoną na zbiorze liczb rzeczywistych taką, że:
F(x) = P(X <= x) | (2.2.1) |
Z określenia dystrybuanty wynikają następujące jej własności:
1) 0 <= F(x) <= 1, dla x Î R
2) limx->ooF(x) = 0 oraz limx->oo F(x) = 1
3) Dystrybuanta jest funkcją niemalejącą, to znaczy, że dla dowolnych x
1 i x2 takich, że x1 < x2 zachodzi nierówność F(x1)<=F(x2).Uwaga:
W niektórych podręcznikach przy określaniu dystrybuanty wprowadza się zamiast 2.2.1 definicję: F(x) = P (X < x).
Przykład 2.5Przykład 2.62.3 Rozkład zmiennej losowej skokowej
Niech wartościami zmiennej skokowej X będą: x1, x2, ..., xn, ..., prawdopodobieństwa zaś z jakimi realizuje ona te wartości niech będą odpowiednio: p1, p2, ..., pn, .... Funkcją rozkładu prawdopodobieństwa (w skrócie funkcją rozkładu) zmiennej losowej skokowej X nazywamy funkcję określoną wzorem:
| (2.2.2) |
Fakt, że powyższy wzór określa funkcję, możemy zapisać: f(xi ) = pi. Można więc powiedzieć, że funkcja rozkładu prawdopodobieństwa zmiennej losowej skokowej X to zbiór par (xi, pi) dla i = 1,2, ..., gdzie xi są wartościami tej zmiennej, a pi prawdopodobieństwami im odpowiadającymi. Funkcja rozkładu zmiennej losowej może być dana za pomocą wzoru, tabeli lub wykresu. Dystrybuantę zmiennej losowej skokowej X można wyrazić wzorem:
| (2.2.3) |
Zauważmy, że dystrybuanta jednoznacznie określa rozkład zmiennej losowej. A zatem rozkład zmiennej losowej skokowej można opisać podając albo funkcję rozkładu prawdopodobieństwa, albo dystrybuantę.
Przykład 2.7Przykład 2.82.4 Rozkład zmiennej losowej ciągłej
Jeżeli dystrybuanta F(x) zmiennej losowej ciągłej X ma pochodną f(x) w całym przedziale zmienności X, to pochodną tę nazywamy funkcją gęstości prawdopodobieństwa (f.g.p.) lub krótko funkcją gęstości. Jest więc spełniona równość:
F'(x) = f(x) | (2.4.1) |
F'(x) = f(x)Funkcja gęstości opisuje rozkład zmiennej losowej ciągłej. Z określenia funkcji gęstości widać, że dystrybuanta F(x) jest funkcją pierwotną funkcji gęstości prawdopodobieństwa f(x). A zatem znając funkcję gęstości f(x) zmiennej losowej ciągłej, można wyznaczyć jej dystrybuantę.
Dystrybuanta zmiennej losowej ciągłej X wyraża się wzorem:
| (2.4.2) |
Funkcja gęstości jest w praktyce ciągła w całym obszarze zmienności X, ewentualnie z wyjątkiem co najwyżej skończonej liczby punktów, oraz ma następujące własności:
1) f(x) >= 0
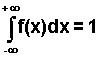 .
.Funkcja gęstości pozwala obliczać prawdopodobieństwo, że wartości zmiennej losowej X należą do dowolnego przedziału o końcach a, b:
| (2.4.3) |
Z powyższego wzoru widać, że prawdopodobieństwo, iż zmienna losowa ciągła przyjmuje wartości z przedziału (a, b) jest równe polu powierzchni pod wykresem funkcji gęstości w przedziale (a, b).
Mamy ponadto bardzo często wykorzystywaną zależność:
P(a < X < b) = F(b) - F(a) | (2.4.4) |
Ponieważ dystrybuanta jednoznacznie określa rozkład zmiennej losowej, zatem rozkład zmiennej losowej ciągłej można opisać albo za pomocą funkcji gęstości prawdopodobieństwa, albo za pomocą dystrybuanty.
Uwaga.
Należy podkreślić, że dla zmiennych losowych ciągłych nie mówi się o prawdopodobieństwie realizacji przez zmienną konkretnej wartości. Ponieważ prawdopodobieństwo, że zmienna losowa ciągła przyjmuje konkretną wartość zawsze równe jest 0: P(X=x0)= 0
Stąd też:
P(a < X < b) = P(a <=X < b) = P(a < X <=b) = P(a <=X <=b) | (2.4.5) |
2.5 Parametry rozkładów zmiennych losowych
W praktyce ważne znaczenie ma scharakteryzowanie rozkładu zmiennych losowych za pomocą pewnych wartości liczbowych, zwanych parametrami. Rozważać będziemy dwie zasadnicze grupy parametrów:
1) miary położenia - najważniejszą z nich jest wartość oczekiwana E(X) (wartość średnia, przeciętna, nadzieja matematyczna),
2) miary zmienności (rozproszenia, dyspersji) - najważniejsze z nich to wariancja D
2(X) i odchylenie standardowe D(X), będące pierwiastkiem kwadratowym z wariancji.Wartość oczekiwaną rozumiemy jako wartość, wokół której skupiają się realizacje zmiennej losowej uzyskiwane w wyniku wielokrotnie powtarzanego doświadczenia. Wariancja natomiast jest miarą rozproszenia wartości zmiennej wokół wartości oczekiwanej. Im mniejsza jest wariancja, tym bardziej wartości zmiennej skupiają się wokół wartości oczekiwanej.
Dla zmiennej losowej skokowej X parametry te liczymy ze wzorów:
Wartość oczekiwana:
| (2.5.1) |
Wariancja:
| (2.5.2) |
Odchylenie standardowe:
| (2.5.3) |
Wariancję dla zmiennej losowej skokowej wygodniej jest liczyć ze wzoru, który otrzymujemy przekształcając postać (2.5.2):
| (2.5.4) |
Dla zmiennej losowej
ciągłej X, której rozkład wyrażony jest przez funkcję gęstości f(x), odpowiednie parametry wyrażają się wzorami:Wartość oczekiwana:
| (2.5.5) |
Wariancja:
| (2.5.6) |
lub po przekształceniu powyższego wzoru wygodniejsza rachunkowo postać:
| (2.5.7) |
Odchylenie standardowe:
| (2.5.8) |
2.6 Ważniejsze rozkłady zmiennych losowych
Do n
ajważniejszych rozkładów skokowych należą: rozkład zero-jedynkowy, rozkład Bernoulliego i rozkład Poissona. Najbardziej znanymi rozkładami ciągłymi są: rozkład równomierny i rozkład normalny.Rozkład zero-jedynkowy (dwupunktowy)
Do ważniejszych rozkładów typu skokowego zaliczamy rozkład zero-jedynkowy. Zmienna losowa X ma rozkład zero-jedynkowy, jeśli przyjmuje tylko dwie wartości: 0 i 1. Wartość 1 z prawdopodobieństwem p i wartość 0 z prawdopodobieństwem q = 1 - p. Rozkład tej zmiennej określają wzory:
P(X = 1) = p, P(X = 0) = 1 - p = q, przy czym p + q = 1 | (2.6.1) |
lub tabela:
xi | 0 | 1 |
pi | q | P |
Parametry rozkładu zero-jedynkowego wynoszą odpowiednio:
E(X) = 0 × q + 1 × p = p | (2.6.2) |
D2 (X) = 02×q + 12 × p - p2 = p - p2 = p (1 - p) = p × q | (2.6.3) |
Zmienna losowa X ma rozkład Bernoulliego, jeśli przyjmuje wartość k (k = 0, 1, 2, ..., n) z prawdopodobieństwem:
| (2.6.4) |
Łatwo zauważyć, że jeśli seria n doświadczeń wykonywana jest zgodnie ze schematem Bernoulliego, to zmienna losowa X określona jako liczba k sukcesów w n doświadczeniach ma rozkład opisany powyżej. Parametry rozkładu dwumianowego wynoszą odpowiednio:
Wartość oczekiwana:
E(X) = n × p | (2.6.5) |
Wariancja:
D2(X) = n × p × (1 - p) = n × p × q | (2.6.6) |
Odchylenie standardowe:
| (2.6.7) |
Kolejnym ważnym rozkładem skokowym jest rozkład Poissona. Znajduje on szerokie zastosowanie m.in. w statystycznej kontroli jakości.
Zmienna losowa X ma rozkład Poissona, jeśli przyjmuje wartość k (k = 0, 1, 2, ..., ) z prawdopodobieństwem:
| (2.6.8) |
Rozkład Poissona dobrze opisuje te doświadczenia losowe, w których obserwujemy dużą serię prób przy małym prawdopodobieństwie sukcesu w pojedynczej próbie. Stąd też, gdy n >= 30 oraz p <= 0,2, rozkład Poissona można stosować jako przybliżenie rozkładu Bernoullie
go, przy czym:l = n × p | (2.6.9) |
Dla rozkładu Poisson'a mamy:
E(X) = l | (2.6.10) |
D2(X) = l | (2.6.11) |
Wartości funkcji rozkładu prawdopodobieństwa dla rozkładu Poissona przy różnych wartościach l oraz dla rozkładu Bernoulliego przy różnych n i p, podane są w tablicach statystycznych (
tablicy1 i tablicy 2).Przykład 2.15Przykład 2.16Przykład 2.17Rozkład równomierny (jednostajny, prostokątny)Powiemy, że zmienna losowa X, określona w przedziale <a, b>, ma rozkład równomierny, jeżeli jej funkcja gęstości prawdopodobieństwa określona jest wzorem:
| (2.6.12) |
Dystrybuanta tej zmiennej ma po
stać:
| (2.6.13) |
Wartość oczekiwana i wariancja w rozkładzie równomiernym wynoszą odpowiednio:
| (2.6.14) |
| (2.6.15) |
Jedny
m z najważniejszych i jednocześnie najczęściej spotykanym w zjawiskach przyrodniczych jest rozkład normalny. Funkcja gęstości tego rozkładu określona jest wzorem:
| (2.6.16) |
dla x Î R, przy czym s
> 0.E(X) = m | (2.6.17) |
D2(X) = s2 | (2.6.18) |
D(X) = s | (2.6.19) |
Fakt, że zmienna losowa X ma rozkład normalny ze średnią m (wartością oczekiwaną) i odchyleniem sta
ndardowym s, będziemy zapisywać symbolicznie w postaci: X ~ N(m; s). Wykresem funkcji gęstości rozkładu normalnego jest tzw. krzywa Gaussa (w kształcie dzwonu, kapelusza). Krzywa ta jest symetryczna względem prostej o równaniu x = m (prostej równoległej do osi y-ów przechodzącej przez punkt m na osi x-ów). W punkcie x = m funkcja osiąga maksimum. Pole powierzchni pod krzywą Gaussa jest równe jeden (co wynika z faktu, że jest to funkcja gęstości prawdopodobieństwa).Położenie i kształt krzywej Gaussa zależy od parametrów rozkładu, czyli od wartości średniej m oraz odchylenia standardowego s. Zmiany m będą powodować przesuwanie wykresu funkcji gęstości wzdłuż osi x-ów bez zmiany jego kształtu, natomiast zmiany odchylenia standardowego będą zmieniać kształt wykresu funkcji bez zmiany jego położenia. Jednoczesne zmiany obu parametrów spowodują zmianę i położenia, i kształtu wykresu funkcji gęstości. Zwiększanie parametru m powoduje przesuwanie wykresu w prawą stronę. Zwiększanie parametru s sprawia, że wykres staje się szerszy i niższy. Wykres funkcji gęstości rozkładu normalnego ma dwa punkty przegięcia (punkty, w których styczna do wykresu funkcji przechodzi z jednej jego strony na drugą). Są to punkty:
x = m - s oraz x = m + s. Odległość między punktami przegięcia jest równa 2s. Jeżeli zmienna losowa X ma rozkład N(m; s) i interesuje nas prawdopodobieństwo, że zmienna ta przyjmie wartości z pewnego przedziału liczbowego np. <a; b>, to teoretycznie musielibyśmy obliczyć wartość całki: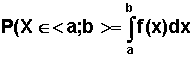
Prawdopodobieństwo to jest równe polu pod wykresem funkcji gęstości ograniczonym osią x-ów i prostymi o równaniach odpowiednio x = a i x = b. W praktyce jednak, aby obliczyć takie prawdopodobieństwo, posługujemy się rozkładem normalnym standaryzowanym, który został stablicowany (
tablica 3).Rozkład normalny standaryzowany
jest to rozkład normalny ze średnią m = 0 i odchyleniem standardowym s = 1.Okazuje się, że dowolną zmienną losową X o rozkładzie norma
lnym z parametrami m oraz s można sprowadzić do zmiennej losowej U o rozkładzie standaryzowanym. W tym celu stosuje się przekształcenie:
| (2.6.20) |
Mamy wówczas: U
~ N(0;1).Funkcja gęstości rozkładu normalnego standaryzowanego jest wyrażona wzorem:
| (2.6.21) |
Funkcja f(u) ma dwa punkty przegięcia: u = -1 oraz u = 1, a jej wykres jest symetryczny względem osi OY. Z symetrii tej wynika, że:
F(-u) = 1 - F(u) | (2.6.22) |
Między wartościami funkcji f(u) i f(x) zachodzi związek:
| (2.6.23) |
a między dystrybuantami:
F(u) = F(x) | (2.6.24) |
Równość dystrybuant rozkładu normalnego i normalnego standaryzowanego umożliwia proste wyznaczanie prawdopodobieństwa przyjęcia przez zmienną losową X wartości z pewnego przedziału liczbowego. W tablicy 3 podane są wartości dystrybuanty zmiennej losowej standaryzowanej dla różnych wartości u.
Przykład 2.19Dla każdego rozkładu normalnego prawdzie są równości:1) P(m - s < X < m + s) = P(-1 < U < 1) = 0,6827 | (2.6.25) |
2) P(m - 2s < X < m + 2s) = P(-2 < U < 2) = 0,9545 | (2.6.26) |
3) P(m - 3s < X < m + 3s) = P(-3 < U < 3) = 0,9973 | (2.6.27) |
Równości te noszą nazwę reguły trzech sigm. Z równości trzeciej wynika, że prawdopodobieństwo przyjęcia przez zmienną losową X o rozkładzie normalnym wartości z przedziału <m-3s
; m+3s> jest bliskie jedności. Oznacza to, że w przedziale <m-3s; m+3s> znajdują się prawie wszystkie wartości zmiennej losowej X. A zatem prawdopodobieństwo przyjęcia przez zmienną losową X wartości spoza tego przedziału jest bardzo małe, praktycznie równe zero.Uwaga:
Zauważmy, że ze względu na ciągłość rozkładu zmiennej X powyższe wzory nie zmienią się, gdy nierówności ostre zastąpimy nieostrymi.
Przykład 2.20Zadania do samodzielnego rozwiązania